본 글은 [A Time Series is Worth 64 Words: Long-Term Forcasting with Transformer] 논문을 한국어로 정리한 것이다.
저작권은 오직 나에게 있음을 명시한다.
Abstract
PatchTST는 다변량 시계열 예측과 지도학습을 위한 트랜스포머 기반의 모델이다.
2개의 핵심요소
(1) 시계열을 여러개의 패치로 분할 → 이 패치를 입력 토큰으로 사용
(2) 하나의 채널에 여러개의 패치가 포함되도록 패치분배 → 각 채널마다 고유한 임베딩과 가중치를 사용 (채널 독립성)

3가지의 이점
- patch가 input이 되기에, 임베딩 계산에서 local 정보가 유지된다
- patch가 input이 되기에, 같은 look-back window를 사용했을 때 어텐션맵의 메모리 사용이 제곱으로 줄어든다. 그 결과, 더 오랜 기간의 데이터를 고려할 수 있다.
- PatchTST를 기존 SOTA 모델과 비교했을 때, 장기적인 예측에 있어 정확도가 현저히 높았다.
Introduction
트랜스포머는 순차적인 데이터 사이의 관계와 연관성을 학습할 수 있는 어텐션 메커니즘을 활용하여 순차적인 데이터를 다루는 문제에 강점을 보인다. 트랜스포머의 사용분야는 NLP, CV, 음성인식을 넘어 최근에는 시계열 분석까지 확장되었다.
Informer, Autoformer, FEDformer는 시계열 분석에 적용할 수 있는 효과적인 트랜스포머 기반 모델로 제안되었으나, 최근 연구에서는 이러한 트랜스포머 모델들보다 간단한 선형모델이 더 우수한 성능을 보이는 여러 경우를 제시하며 시계열 예측에 트랜스포머의 사용이 실제로 유용한지 의문을 제기했다.
이 의문에 대해 이 논문은 2개의 핵심 디자인인 Patching과 Channel-independence 로 답한다.
1. Patching
시계열 예측의 목표는 서로 다른 input 간의 상관관계를 이해하는 것이다. 그렇다면 input을 무엇으로 두어야 할까?
- 기존 모델은 하나의 시점이나 시점들을 가공한 값을 input으로 본다 = point-wise
- PatchTST은 여러 시점들을 패치로 묶고, 패치를 input으로 본다 = patch-wise
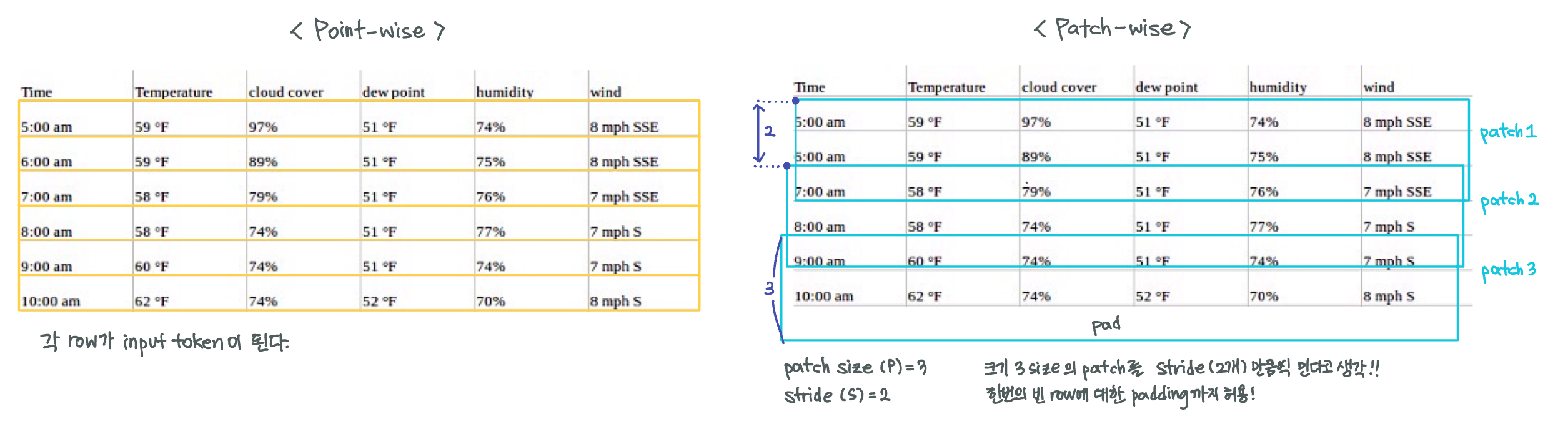
쉽게 말하자면 영어 문장을 이해하기 위해 ‘알파벳 하나씩’ 보는 것보다 주변 local 정보를 담고있는 ’단어 하나씩‘ 보는게 훨씬 낫듯이, 시계열도 ’시점 하나씩‘ 보는 것보다 주변 local 정보를 담는 ’여러 시점을 합친 패치 하나씩‘ 보는게 낫다고 주장한다.
2. Channel-independence
하나의 변수가 하나의 채널을 갖기에, 다변량 시계열은 여러 개의 채널 시그널을 갖는다는 것을 의미한다. 그렇다면 input embedding에 쓰이는 채널의 개수는 어떻게 둘까?
- 기존 모델은 행별로 공통의 embedding space에 통과시켜 여러 채널/변수의 정보를 섞는다 = channel-mixing
- PatchTST는 채널/변수마다 각자의 embedding space가 있어서 여러 변수의 정보가 섞이지 않는다 = channel-independence

채널 독립성이 CNN과 선형모델에는 잘 작동됨이 증명되었으나, 트랜스포머 모델에는 PatchTST가 처음 도입했다고 자랑한다.
Traffic Dataset에 대한 case study 결과
L(look-back window), N(# of input tokens), patch 유무에 따른 MSE를 (1) channel-independent PatchTST와 (2) channel-mixing FEDFormer 모델 2개로 나누어 평가했다.
이를 통해 channel-independent와 channel-mixing의 차이와 patchTST와 기존의 FEDFormer의 차이를 확인할 수 있겠다.

1. 시간과 공간복잡도의 감소
기존 트랜스포머는 입력 토큰의 개수 N에 대해 $ O(N^2) $ 의 시간과 공간 복잡도를 가진다.
패치 적용 전에는, N이 데이터 길이인 L과 같은 값을 가지기에 시간과 공간에 병목 현상이 생긴다.
패치 적용 후에는, \( N = \lfloor \frac{(L-P)}{S} \rfloor + 2 \) 이 되어 \( N \approx \frac{L}{S} \) 이기에 시간과 공간 복잡도 \( O(N^2) \)는 \( O(\frac{L}{S}^2 \) 가 되어 S의 제곱만큼 감소한다. (S는 stride로 쉽게말해 patch의 이동간격라고 보면 된다.)
우측 테이블에서 dataset ‘Traffic’을 살펴보면, patch를 사용했을 때의 러닝타임 (464)가 patch를 사용하지 않았을 때의 러닝타임 (10040)보다 대략 22배 빠르다는 것을 보일 수 있다.
2. 더 긴 L(look-back window : 과거 데이터 참조 범위) 사용 가능
좌측 테이블에서 첫 2개의 행을 보면 L을 96에서 380으로 늘렸을 때, MSE가 0.518에서 0.447로 감소함을 통해, L(데이터의 개수)=N(input token 개수)를 늘리면 MSE가 줄어든다는 것을 알 수 있다.
그렇다고 지금같이 \( L=N \)인 상황에서 L을 무턱대고 늘리면 N도 커져서 메모리 사용량과 계산량이 심각하게 많아진다.
흠… 그렇다면 L을 늘리면서 N을 유지시킬 수 있는 방법은 없나…?
있다! Patch TST는 patch로 이 문제를 해결한다.
patch를 사용한다면 L을 늘려도 \( N \approx \frac{L}{S} \) 이기에 N은 대략 S(stride)로 나눈만큼 줄어든다. 그렇다면 S의 도입으로 N의 커짐을 막고, N의 커짐을 막으면 메모리 사용량과 계산량도 지킬 수 있다.
좌측 테이블의 3번째와 4번째 행을 통해 같은 L size여도 patch를 적용했을 때, N이 336에서 42로 줄어들면서 MSE도 0.397에서 0.367로 낮아짐을 보일 수 있다.
3. Representation Learning 사용 가능
비지도학습에서 데이터의 abstract representation을 포착하려면 유연한 모델을 사용해야한다.
좌측 테이블의 5번째 행을 통해 비지도학습인 PatchTST에 대해서 가장 뛰어난 MSE값인 0.349를 가지므로, PatchTST는 예측도 되고 경향성도 잘 뽑아낸다고 자랑하고 있다.
Related Work
1. 다른 분야에서도 local 정보가 중요하면 patching을 사용했다
- NLP : BERT는 tokenization에 character-based가 아닌 subword-based 를 택했다.
- CV : ViT는 이미지를 16X16 사이즈의 패치로 나누고 이를 input으로 썼다, BEiT과 masked autoencoders도 패치를 input으로 썼다.
- 음성지원 : 오디오를 부분적으로 추출하기 위해 convolution(합성곱)을 사용한다. 일종의 패치화.
2. 트랜스포머 기반 장기 시계열 예측
과거에도 시간과 공간 복잡도를 줄이기 위해 L을 늘리면서 N을 유지시킬 수 있는 방법의 고민이 있어왔다. 각 모델들의 타파방법을 알아보자.
N을 건들지 않고 중간과정의 불필요한 계산을 줄이는 방법으로 시간과 공간 복잡도를 줄이는 경우 \( O(N^2) \)
- LogTrans: LogSparse 디자인의 convolusional self-attention을 사용
- Informer: ProbSparse self-attention의 사용으로 중요한 K만 효율적으로 선택
- Autoformer: 전통적인 시계열 분석에 쓰이는 decomposition과 auto-correlation 개념을 사용
N을 건들여서 시간과 공간 복잡도를 선형적으로 줄이는 경우 \( O(N^2) \rightarrow O(N) \)
- FEDformer: 푸리에 강화구조를 사용
- Pyraformer: 피라미드 어텐션 모듈을 적용
3. 시계열 Representation Learning
representation learning인 경향성 파악에 비지도학습은 중요한 연구 토픽이다.
최근 시계열 데이터에서 representation을 학습하는 트랜스포머 기반이 아닌 모델이 제안되었지만, 우리는 트랜스포머도 쟁쟁한 후보가 될 수 있다고 생각한다 ! 아직 트랜스포머의 잠재력이 전부 발휘되지 않았다 !!
Proposed Method
Model Structure
논문의 내용을 이해하기 쉽게 대략 7단계로 각색하였다.

1. M개의 변수 column을 전부 하나의 행으로 떼버린다.
2. patching 전에 \(x_L^{(i)} \)
